PID-Regler werden zur Beeinflussung bestimmter Messgrößen eingesetzt. Als clevere 3-in-1 Regler bewähren sie sich tagtäglich in zahlreichen Industriesystemen und regeln sehr präzise auf den Sollwert. Bei uns erfahren Sie die wichtigsten Daten und Fakten rund um die PID-Regelung.
Ein Kompaktregler lässt sich an die unterschiedlichsten Anwendungen anpassen und findet in der Regel als PID-Regler Verwendung. Er arbeitet proportional, integrierend und differenzierend (PID), wobei die Intensität der einzelnen Anteile an die Regelstrecke angepasst wird. Dies geschieht über die Dimensionierung der Regelparameter
Das Prinzip eines PID-Reglers ist relativ einfach zu erklären. Ob beispielsweise als PID-Temperaturregler oder PID-Feuchteregler – es wird immer versucht, eine bestimmte Regelgröße anhand des Istwerts auf den Sollwert auszuregeln. Dabei verstärkt der P-Regler die Regeldifferenz, der I-Anteil vergrößert seinen Stellgrad bei vorhandener Regelabweichung und der D-Regler wirkt der Bewegung des Istwertes entgegen. Werden nicht alle Anteile für die Regelung benötigt, können diese deaktiviert werden. Je nach Anwendung werden sie dann als PI-Regler, P-Regler, PD-Regler oder I-Regler benannt.
Für die meisten Anwendungen weist die PID-Struktur das beste Regelverhalten auf. So sind PID-Kompaktregler sehr verbreitet im Bereich von Temperaturregelungen, sie ermöglichen auch den direkten Anschluss von Widerstandsthermometern und Thermoelementen. Einige Regelgrößen erfordern das Deaktivieren bestimmter Anteile, darunter u. a. Drehzahl und Durchfluss.
Der P-Anteil reagiert sehr schnell und verstärkt die Regeldifferenz, nachteilig wirkt sich seine bleibende Regelabweichung aus. Der verantwortliche Regelparameter ist der Proportionalbereich Xp. Mit kleiner dimensioniertem Xp wird der Regler schneller und die Regelabweichung geringer. Das Gesamtsystem neigt aber immer mehr zum Schwingen.
Der I-Anteil beseitigt die Regelabweichung. Wird die Nachstellzeit Tn kleiner eingestellt, baut der Regler schneller seinen Stellgrad auf und wirkt auch schneller der Regelabweichung entgegen. Bei zu kleiner Einstellung kommt es allerdings ebenfalls zu einem schwingenden Verhalten.
Der D-Anteil wirkt der Bewegung des Istwertes entgegen. Das bedeutet für einen Regler zum Heizen, dass der Anteil bei steigendem Istwert reduziert und bei sinkendem Istwert erhöht wird. Das beschriebene Verhalten wirkt dämpfend. Der verantwortliche Parameter ist die Vorhaltezeit Tv. Je größer Tv eingestellt ist, umso größer ist die beschriebene Wirkung.
Das Verhalten von Regelstrecken ist immer arbeitspunktabhängig. Zur Optimierung muss das System in einen Betriebszustand gebracht werden, für den später günstige Regelparameter erwartet werden. Beispielsweise wird ein Ofen vor der Optimierung beladen, während für einen Durchlauferhitzer eine Abnahme generiert werden muss. Muss bei der Optimierung ein Zielwert vorgegeben werden, liegt dieser später im Arbeitsbereich
Existieren vergleichbare Anlagen/Regelkreise, können versuchsweise die dort verwendeten Regelparameter
Einsatz finden. Führt dieser Ansatz nicht zum Ziel, kann eines der folgenden Optimierungsverfahren eingesetzt werden.
Schwingungsmethode nach Ziegler und Nichols
Dieses Verfahren findet für relativ schnelle Regelstrecken Verwendung. Zur Vorbereitung wird die P-Struktur parametriert und ein relativ großes Xp eingestellt. Ein Sollwert im späteren Arbeitsbereich wird in der nachfolgenden Abbildung definiert.
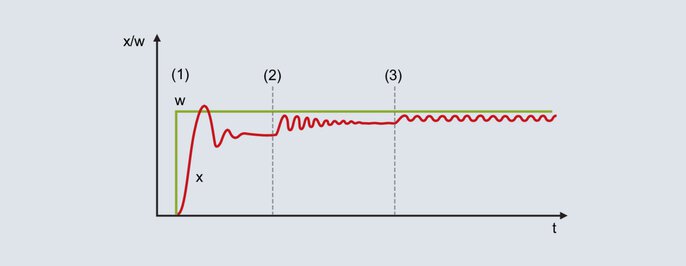
Abb. 52: Sollwert- und Istwertverlauf bei Anwendung der Schwingungsmethode
Mit dem relativ groß eingestellten Proportionalbereich läuft der Istwert mit geringer Schwingungsneigung auf den Endwert [Abbildung 52 (1)]. Aufgrund der nicht vorhandenen I-Struktur ist eine dauerhafte Regelabweichung vorhanden.
Das Xp wird verkleinert (Abbildung 52 [2]): Der Istwert steigt an und läuft mit größerer Schwingungsneigung auf den Endwert. Der Proportionalbereich wird unter Umständen mehrmals verkleinert, bis der Istwert dauerhaft schwingt (Abbildung 52 [3]). Der für dieses Verhalten erforderliche Proportionalbereich wird als Xpk (kritisches Xp) bezeichnet und ist möglichst genau zu bestimmen (Xp nicht in zu großen Schritten verkleinern).
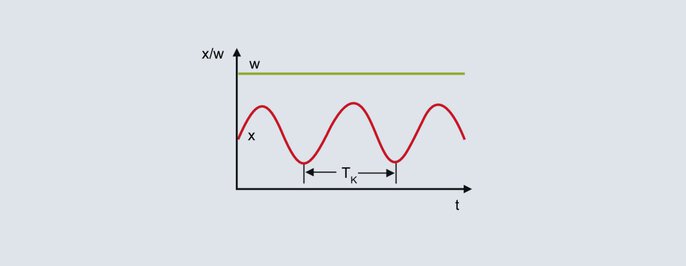
Kritische Periodendauer
Aus der Dauerschwingung des Istwertes in der oberen Abbildung wird mit der kritischen Periodendauer Tk die zweite Kenngröße für das Verfahren bestimmt. Die kritische Periodendauer Tk (in Sekunden) ergibt sich beispielsweise durch den zeitlichen Abstand zwischen 2 Minimalwerten. Zur Bestimmung der Regelparameter werden Xpk und Tk in die folgende Tabelle für die gewünschte Reglerstruktur eingesetzt.
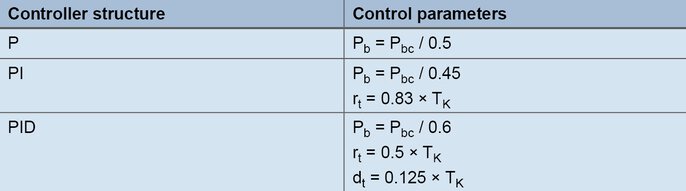
Formeln zur Einstellung nach der Schwingungsmethode
Verfahren nach der Streckensprungantwort nach Chien, Hrones und Reswick
Mit diesem Verfahren werden die Regelparameter auch für träge Regelstrecken relativ zeitsparend ermittelt. Die Methode wird für Strecken ab 2. Ordnung angewendet und bietet die Besonderheit der Unterscheidung zwischen den Formeln für das Führungs- und Störverhalten. Für die Faustformeln werden aus der Sprungantwort der Übertragungsbeiwert der Regelstrecke, die Verzugs- und die Ausgleichszeit ermittelt.
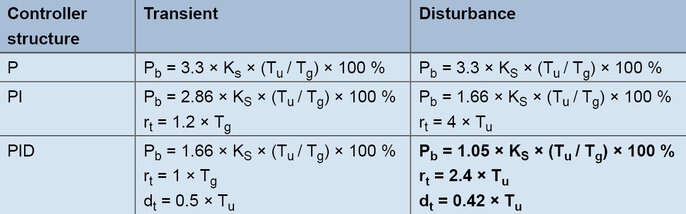
Formeln zur Erstellung nach der Streckensprungantwort
Beispiel:
Für einen Laborofen soll ein Regler mit PID-Struktur eingesetzt werden. Ziel ist ein gutes Störverhalten, typische Sollwerte liegen bei 200 °C. Im Handbetrieb wird der Stellgrad stufenweise erhöht, bis sich ein etwas unter dem späteren Sollwert liegender Istwert ergibt (die Ausgleichsvorgänge sind jeweils abzuwarten). Beispielhaft wird mit einem Stellgrad von 60 % eine Temperatur von 180 °C erreicht. Von 60 % ausgehend, wird der Stellgrad sprungförmig auf 80 % erhöht und der Istwert aufgezeichnet.
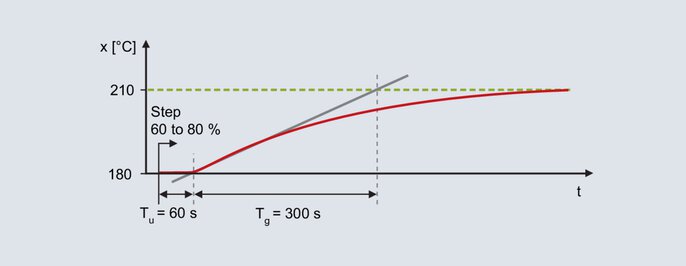
Sprungantwort des Laborofens
Aus der Sprungantwort wird mithilfe der Wendetangente ermittelt: Verzugszeit Tu = 60 s, Ausgleichszeit Tg = 300 s. Der Übertragungsbeiwert der Regelstrecke ergibt sich aus der Veränderung des Istwertes, dividiert durch den Stellgradsprung.
Gleichung 22
Mithilfe der Faustformeln ergeben sich folgende Parameter für das Störverhalten:
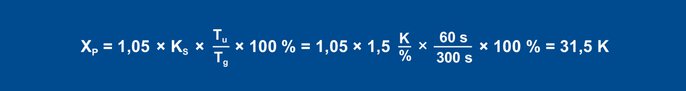
Gleichung 23
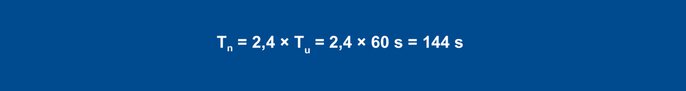
Gleichung 24
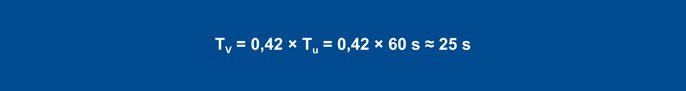
Gleichung 25
Der Stellgradsprung ist im Bereich des späteren Arbeitspunktes durchzuführen. Die Sprunghöhe ist weiterhin so groß zu wählen, dass der Istwertverlauf ausgewertet werden kann. Nach der Vorgabe des Stellgradsprunges wird der Endwert des Istwertes abgewartet, eine Zeit sparende Alternative bietet das Verfahren nach der Anstiegsgeschwindigkeit.
Verfahren nach der Anstiegsgeschwindigkeit
Hinsichtlich der Sprungvorgabe erfolgt die Vorgehensweise wie beim Verfahren nach der Streckensprungantwort. Vor dem Sprung wird ein Stellgrad vorgegeben, mit welchem der Istwert etwas unterhalb des später verwendeten Sollwertes liegt.
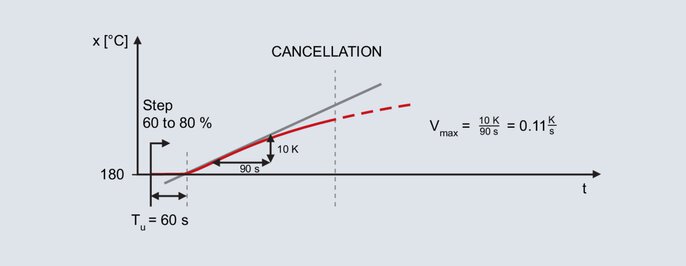
Istwertverlauf beim Verfahren nach Anstiegsgeschwindigkeit
Die Sprungvorgabe erfolgt erneut für den bereits erwähnten Laborofen; der spätere Arbeitspunkt liegt ebenfalls bei 200 °C. Durch die Vorgabe eines Stellgrades von 60 % im Handbetrieb ergibt sich ein Istwert von 180 °C. Der Stellgrad wird sprungförmig auf 80 % erhöht.
Nach Vorgabe des Sprunges steigt der Istwert nach einiger Zeit an. Die Aufzeichnung erfolgt, bis der Istwert seine maximale Steilheit aufweist. Auch bei diesem Verfahren wird die Wendetangente eingezeichnet und die Verzugszeit ermittelt. Die zweite Kenngröße ist die maximale Anstiegsgeschwindigkeit, diese entspricht der Steigung der Wendetangente. Durch ein Steigungsdreieck an der Wendetangente wird die maximale Anstiegsgeschwindigkeit bestimmt:
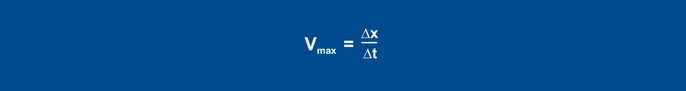
Gleichung 26
Die ermittelten Werte Vmax (0,11 K/s) und Tu (60 s) werden in folgende Formeln eingesetzt:
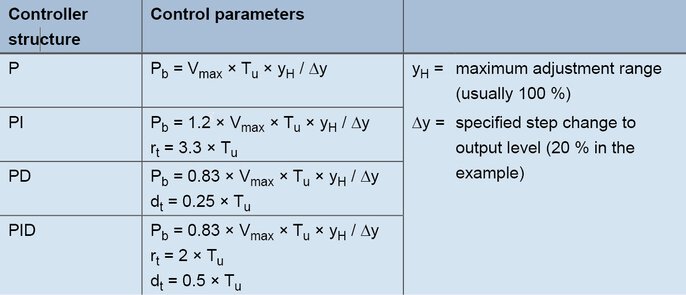
Formeln zur Einstellung nach der Anstiegsgeschwindigkeit
Für einen PID-Regler ergeben sich die Werte mit den Formeln wie folgt:
Gleichung 27
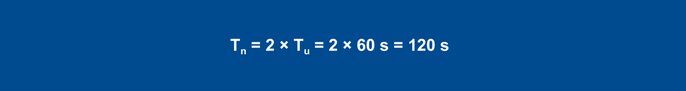
Gleichung 28
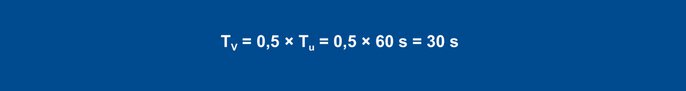
Gleichung 29
Empirische Methode zur Ermittlung der Regelparameter
Mit diesem Verfahren werden nacheinander günstige Einstellungen für die Anteile P, D und I ermittelt. Vom Ursprungszustand aus (Stellgrad 0 %) gibt man immer wieder den typischen Sollwert vor; daher ist das Verfahren nur für relativ schnelle Regelstrecken anwendbar (z. B. schnelle Temperaturregelstrecken und Regelgrößen wie Drehzahl oder Durchfluss).
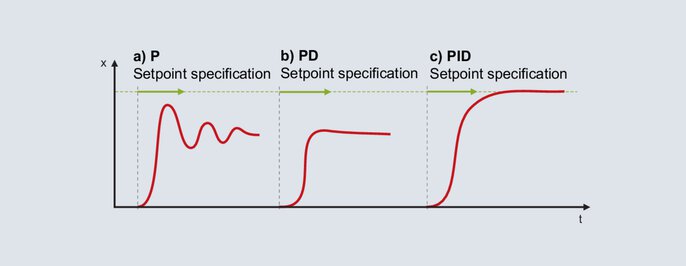
Einstellung eines PID-Reglers nach der empirischen Methode
Für den Regler wird die P-Struktur aktiviert. Der Proportionalbereich wird relativ groß eingestellt (die Dimensionierung hängt von der Regelstrecke ab) und der Sollwert im späteren Arbeitsbereich vorgegeben. Der Istwert wird träge auf den Endwert laufen und es ergibt sich eine relativ große Regelabweichung. In der Folge wird der Sollwert mit einem immer kleiner werdenden Proportionalbereich Xp vorgegeben. Ziel ist ein Xp, bei dem der Istwert nach 2 bis 3 Vollschwingungen seinen stabilen Endwert erreicht (Abbildung 56a). Für ein gedämpftes Anfahren erfolgt die Strukturumschaltung von P auf PD. Beginnend mit einer kleinen Einstellung für die Vorhaltezeit, erfolgt die Sollwertvorgabe mit immer größer werdenden Tv. Erreicht der Istwert seinen Endwert mit einer möglichst kleinen Schwingung, liegt ein günstiges Tv vor (Abbildung 56b).
Hinweis: Sobald der Regler beim Anfahren den Stellgrad auch nur einmal auf 0 % setzt, ist das Tv zu groß eingestellt.
Mit der Umschaltung auf PID-Struktur wird der I-Anteil aktiviert. Die Nachstellzeit Tn ist in der Regel mit dem vierfachen Wert des zuvor ermittelten Tv günstig eingestellt. Abbildung 56c zeigt das Verhalten für eine Einstellung Tn = 4 × Tv.
Für einige Strecken können nicht alle Anteile aktiviert werden. Ergibt sich bei einer P-Struktur bereits für große Einstellungen von Xp ein unruhiges Verhalten, können weder P- noch D-Struktur Verwendung finden. Zum Einsatz kommt der I-Regler.
War die Optimierung des P-Reglers erfolgreich, macht aber die Einführung des D-Anteils den Regelkreis instabil, findet die PI-Struktur Verwendung.
Die Anwendung der vorgestellten Optimierungsverfahren wird sehr wahrscheinlich ein stabiles, aber nicht optimales Regelverhalten herbeiführen. Durch eine manuelle Nachoptimierung wird das Regelergebnis weiter verbessert. Kann das Verhalten eines PID-Reglers einer der Kurven 62b bis 62e zugeordnet werden, finden Sie nachfolgend Hinweise für eine weitere Optimierung.
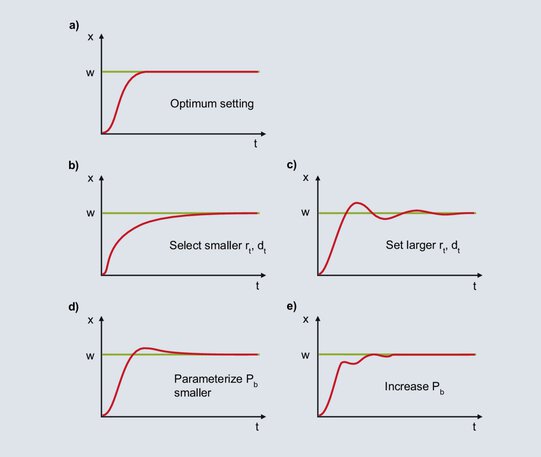
Abb 62: Hinweise zur Nachoptimierung eines PID-Reglers
Das Diagramm zeigt ein optimales Verhalten für einen PID-Regler.
Nach Vorgabe des Sollwertes steigt der Istwert bis zum Erreichen des Proportionalbereiches steil an. Gelangt der Istwert in den Proportionalbereich, wird der P-Anteil reduziert und der I-Anteil sorgt für das Ausregeln auf den Sollwert. Die Vergrößerung des I-Anteils geschieht aufgrund des relativ groß eingestellten Tn träge und die Regelabweichung wird langsam beseitigt. Für das schnellere Aufintegrieren ist Tn kleiner einzustellen; entsprechend dem Verhältnis Tv/Tn = 1/4 wird Tv ebenfalls verkleinert.
Mit dem Eintreten des Istwertes in den Proportionalbereich erhöht der I-Anteil den Stellgrad. Die Vergrößerung hält an, bis der Istwert den Sollwert erreicht. Im dargestellten Fall baut der I-Anteil bis zur Beseitigung der Regelabweichung zu viel Stellgrad auf, der Istwert gelangt über den Sollwert. Mit Vorliegen einer negativen Regelabweichung wird der Stellgrad zu schnell reduziert, der Istwert gelangt unter den Sollwert usw. Die symmetrische Schwingung des Istwertes um den Sollwert lässt auf ein zu klein eingestelltes Tn schließen. Tn muss vergrößert und Tv ebenfalls entsprechend dem Verhältnis Tv / Tn = 1/4 erhöht werden.
Der I-Anteil wird vom Eintreten des Istwertes in den Proportionalbereich bis zur Beseitigung der Regelabweichung gebildet. Aufgrund des groß eingestellten Xp beginnt der I-Anteil bereits bei einer großen Regelabweichung mit der Bildung des Stellgrades. Durch die zu Beginn große Regelabweichung bildet der I-Anteil seinen Stellgrad relativ schnell. Mit der Beseitigung der Regelabweichung steht ein zu großer I-Anteil an, der Istwert gelangt über den Sollwert. Mit einer kleineren Einstellung für Xp beginnt der I-Anteil erst bei kleineren Regelabweichungen entsprechend langsamer mit dem Aufbau seines Stellgrades. Das dargestellte einmalige Überschwingen wird unwahrscheinlicher.
Mit einem zu klein eingestellten Xp wird der Stellgrad des P-Anteils kurz vorm Erreichen des Sollwertes reduziert. Mit Eintreten des Istwertes in den Proportionalbereich wird der P-Anteil sehr stark verkleinert und der Istwert fällt ab. Aufgrund der größeren Regelabweichung wird der Stellgrad größer und der Istwert steigt an. Im Proportionalbereich führen kleine Istwertänderungen zu großen Änderungen des Stellgrades, was in einer hohen Schwingungsneigung resultiert. Eine Beruhigung erfolgt durch die Vergrößerung des Proportionalbereiches.
